ハッシュ関数とMAC - d'space

---

ハッシュ関数とMAC

ハッシュ関数

任意の長さの文字列をある固定長の文字列に（不可逆に）圧縮する関数をハッシュ関数という。

• H : {0,1}* → {0,1}^k

ただし、暗号技術では、ハッシュ関数Hに対し以下の安全性条件を要求する。

原像困難性:
与えられた文字列 y に対し、その原像 x 、すなわち H(x) = y となる x を求めることは計算量的に困難である。

第２原像困難性:
与えられた文字列 x に対し、その第２原像 x' 、すなわち H(x') = H(x)となる、 x とは異なる x' を求めることは計算量的に困難である。

衝突困難性:
衝突ペア (x, x')、すなわち H(x) = H(x')となる、異なる x と x' のペアを求めることは計算量的に困難である。

バースデイ・パラドックス

N個のボールが袋に入っている。各ボールはh個の色のどれかに塗られている。色の分布に偏りはない。

この袋に同じ色のボールが２個以上入っている確率はどの程度だろうか？

• ボールのペアの総数は N(N-1)/2で、N²程度。
• ランダムなペアが同じ色である確率は、1 / h.

よって、袋に同じ色のボールが２個以上入っている確率は、 N² / h 程度。N が h^1/2 程度以上になると無視できない。

nビット出力のハッシュ関数について、

• 2^n/2程度のランダム文字列のハッシュ値を計算すると、ほぼ確実に衝突ペアがみつかる。
• つまり、nビット出力のハッシュ関数の衝突困難性は高々 n/2 ビットである。

マークル・ダムガード変換

固定長入力の

• 圧縮関数 h : {0,1}^2l → {0,1}^l

を以下のように繰り返し用いて、ハッシュ関数 H を構成する方法をマークル・ダムガード変換という：

マークル・ダムガード変換:

• 入力： x
  • (ただし、 x ∈ {0,1}^*, L = |x| < 2^l)
• B = [L/l]
• (x₁, x₂, ・・・, x_B) = x
• x_B+1 = L
• z₀ = 0^l
• for i ∈ [1..(B+1)] :
  • z_i = h(z_i-1 || x_i)
• return z_B+1.

圧縮関数Fが衝突困難性をもつならば、それをマークル・ダムガード変換して得られるハッシュ関数Hも衝突困難性をもつ。

SHA-1

160ビット出力ハッシュ関数

• SHA-1 : {0,1}* → {0,1}¹⁶⁰

は、圧縮関数

• F : {0,1}¹⁶⁰ x {0,1}⁵¹² → {0,1}¹⁶⁰
• F(w, x) = F₀(w, x) + w

をマークル・ダムガード変換して得られる。（'+'は32ビットブロックごとの算術加算）

圧縮関数F₀:
入力：　w = (a,b,c,d,e),　x = (x₀,...,x₁₅)

• ※ 「鍵スケジュール」
• i ∈ [16..79] :
  • x_i = ROTL¹(x_i-3 x_i-8 x_i-14 x_i-16)
  • ※ SHA-0 では ROTL¹ がなかった。
• i ∈ [1..4] :
  • j ∈ [0..19] :
    • t = ROTL⁵(a) + f_i(b,c,d) + e + x_20(i-1)+j + k_i
    • ※ k_iはある定数。
    • e = d,　 d = c,　 c = ROTL³⁰(b),　 b = a,　 a = t
• return (a,b,c,d,e).

圧縮関数 F₀ が各段で用いる撹拌関数 f_i は、

• f₁(b, c, d) = if b then c else d
• f₂(b, c, d) = b c d
• f₃(b, c, d) = (b AND c) OR (c and d) OR (d and b)　※ majority
• f₄(b, c, d) = b c d.

• 基本は、５ブランチのFeistel構造。
• 撹拌関数にコストをかけない。その代わり、ラウンド数を多くする。
• メッセージは「部分鍵」に相当。しかし、「鍵スケジュール」部は単純。大丈夫か？

SHA-1の局所衝突

　　　↑
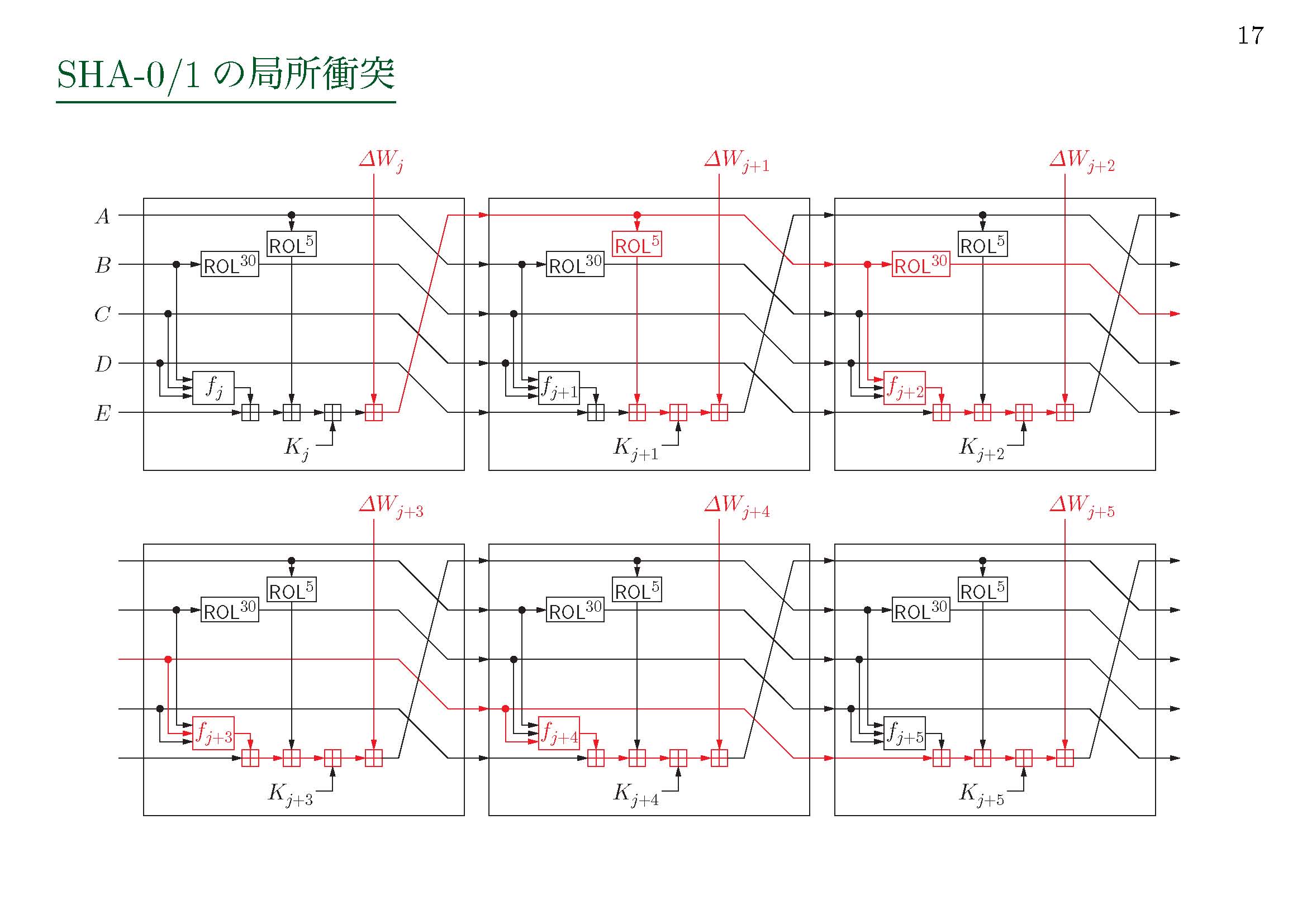
第5回ISS スクエア水平ワークショップ(2008/12/19, 情報セキュリティ大学院大学)　廣瀬勝一「ハッシュ関数の標準化と最新動向」より抜粋させて頂きました。

• 関連鍵攻撃の発見という形で、ブロック暗号へも波及。歴史は繰り返す。

SHA-xの動向

• 1995年 - SHA-1 （FIPS 180-1、NIST)
• 2002年 - SHA-256/384/512　（FIPS 180-2、NIST)
• 2005年 - SHA-1に衝突攻撃
• 2007年 - Cryptographic Hash Competition（NIST）→ SHA-3（2012）
• 2012年 - SHA-3 に Keccak が選定

MAC

関数

• M : {0,1}ⁿ {0,1}* → {0,1}ⁿ

が MAC（メッセージ認証コード）であるとは、

• k を知っていたら、どんな m についても t = H_k(m) を容易に計算できる。
• k を知らなかったら、t*=H_k(m*) となるペア (m*, t*) は計算できない。

ことをいう。

ただし、

• 各メッセージの長さは任意。
• ２番目の条件で、攻撃者はオラクルからメッセージとMACのペア (m_i,t_i)を適応的に複数入手できるとする。もちろん、m* ≠ m_i でなければならない。

ハッシュ関数 → MAC

Hをハッシュ関数とする。

単に、

• 関数 m H(k || m)

を（鍵kのメッセージmに関する）MACとして用いると安全でない。

Hが圧縮関数 F からマークル・ダムガード変換で作られているとする。（簡単のため、鍵の長さはブロック長に等しいとする。）

1. x₁ を任意に選び、オラクルに問い合わせ、h = F(F(k, IV), x₁) を得る。
2. x₂ を任意に選び、h' = F(h, x₂) を計算し、((x₁,x₂), h') を出力。

つまり、 ハッシュ値 h が、関数Hの計算状態を保存していて、攻撃者に計算の再開を許してしまう。

HMAC

HMACは、ハッシュ関数 H : {0,1}* → {0,1}ⁿ からMACを安全に構成する方法。

• HMAC_{k1, k2}(m) = H(k₁ || H(k₂ || m))

ハッシュ関数 H が衝突困難で、関数 m H(k₂ || m) が固定長メッセージについて安全なMACであるならば、HMACは安全なMACとなる。

実際にSSLで用いるときは、

• k₁ = k opad
• k₂ = k ipad

としている。 opad、ipad はある文字列。

関連鍵攻撃は大丈夫？

疑似ランダム関数

ランダム関数と計算量的に識別できない関数を疑似ランダム関数と呼ぶ。

SSLでは、ハッシュ関数は疑似ランダム関数としても使われている。より具体的には、マスター秘密から一連の鍵を構成するのに用いられる（鍵導出関数）。

鍵ブロック :=

• MD5(S_master || SHA1("A" || S_pre || R_server || R_client)) ||
• MD5(S_master || SHA1("BB" || S_pre || R_server || R_client)) ||
• MD5(S_master || SHA1("CC" || S_pre || R_server || R_client)) || ・・・

ハッシュ関数は仕事が多くて、たいへんである。

上へ

---